Stripping torques in human bone can be reliably predicted prior to screw insertion with optimum tightness being found between 70% and 80% of the maximum

Article focus

• To find the optimum tightness for non-locking screws as a percentage of the stripping torque (T_str).

• To test for an overall effect of screw tightness on compression and pullout force.

Key messages

• Bone characteristics and screw geometries can be used to predict the maximum torque for a screw hole in human bone prior to insertion, with 70% to 80% of the maximum torque providing optimum screw tightness.

• Having a targetable torque for screw insertion should reduce rates of screw stripping and improve fixation constructs.

• Stripping screw holes reduces pullout force and compression by more than 90%.

Strengths and limitations

• Automated screw insertion ensured that surgical technique was eliminated as a confounder.

• Ex vivo testing on diaphyseal cortical fixation - results need validation in other bone regions.

• Methods used are only an assessment of the immediate implantation consequences and offer no assessment of healing effects, or of changes in constructs as stress dissipates over time and under loading.

Introduction

Non-locking screws continue to play a crucial role in the operative management of the more than nine million fractures estimated to occur worldwide each year.¹ However, the insertion of non-locking screws by surgeons is subjectively controlled and frequently suboptimal; biomechanical evaluations of screw insertion commonly show overtightening or stripping of the surrounding bone.² When screw holes are stripped, the fixation strength is greatly reduced, and this lack of awareness of the torsional limits in the bone, together with the inability to detect them by surgeons, contributes to fixation failures.³ If stripping occurs and is detected, larger screws can be used in the same hole in an attempt to rescue the situation, though this can have limited success.⁴ Alternatively, screws might have to be sited elsewhere, leaving the empty, stripped screw hole to act as a stress riser.⁵ Operating time and implant wastage both increase when screws are inserted poorly.⁶ As stripping torques (T_str) are manually unpredictable and excessive torques result in irreversible construct damage,^4,7 to reduce the risk of stripping the optimum and maximum torques for a screw hole would ideally be known for a chosen screw prior to its insertion. Additionally, knowing the optimum torque to target could potentially lead to better outcomes due to more robust constructs being created, which are able to offer more compression and greater resistance to failure during loading.

Currently, there is a scarcity of research into methods for creating optimum non-locking screw fixations in human bone, with data available only from bovine models without known tightness to target in human bone. In bovine bone, screw tightness greater than 80% of T_str offers no further benefits to fixation, in terms of compression generated or pullout force resisted, and rather increases the risk of stripping the bone.⁷ Methods for predicting T_str have been investigated such as using the torque required to advance a screw during insertion, before the screw head contacts the plate or bone – the plateau torque (T_plat). This has shown during automated insertion to be a strong predictor for T_str for cancellous human bone (n = 80; R² = 0.84; p < 0.001, simple linear regression).⁸

The aim of this study was to quantify and optimize tightness for the insertion of cortical fracture-fixation screws, based on bone characterization and screw geometry. We hypothesized that submaximal torques would generate optimum constructs as a function of compression and pullout force, and that these methods could provide justification for targeting a safe range of torques that reduce the risk of bone stripping.

Methods

Cortical bone rings were made from the diaphysis of a single human cadaveric tibia (female, aged 78 years, body mass index 24 kg/m²) by longitudinal sectioning into 15 rings. This was procured under local ethical approval and stored in vacuum packaging at -20°C in the institutional tissue bank, being defrosted for 18 hours prior to use. All soft tissues were removed alongside all cancellous bone from the medullary cavity of the rings. Each ring had pilot holes of 2.5 mm diameter drilled perpendicularly to the bone surface using an automated bench drill. Pilot holes were spaced approximately 18 mm apart,⁹ with drill bits changed after 20 holes, with a total of 86 holes created. The cortical thickness at the site of each pilot hole was measured with digital Vernier’s callipers from both the proximal and distal aspects, with the mean value recorded.

Establishing experimental T_str

Equation 1 ¹⁰ predicts T_str of a homogeneous sample based on the material properties and screw geometries. To employ this equation, it first required identification of the unknown material variables (cortical thickness, tensile yield stress (TYS), and the coefficient of friction between screw and bone).

T s t r = T Y S √ 3 π ∙ D p ∙ L ∙ r ∙ p + 2 f ∙ r 2 r - f ∙ p

Where TYS = tensile yield stress, D_p = pitch diameter, L = axial length of full thread engagement, r = pitch radius of screw, p = reciprocal of threads per unit length, and f = coefficient of friction between the screw and bone.

The screw geometries remained the same throughout the calculations, as identical screw threads were engaged for all tests: fully threaded, cortical screws, 3.5 mm in outer diameter, made of stainless steel (DePuy Synthes, Zuchwil, Switzerland). The material properties of the bone (TYS and f) were considered to be the same for all tests as the tibia tested was from one individual. Finally, as the cortical thickness was directly measured for each hole, only the TYS and friction coefficient (f) remained as unknown variables. To calculate these, 20 holes from four samples evenly distributed along the length of the tibia (samples 1, 5, 10, and 15 of 15) were used for destructive testing to establish the relationship between cortical thickness (independent variable) and T_str (dependent variable); the rest of the samples were used for submaximal tightness testing. T_str was defined as the maximum torsional force that could be generated when rotating a screw. Screws were initially inserted by hand, through a compression load washer, mounted on bearings. Screw lengths were chosen to ensure that at least 2 mm of screw threads had passed through to the inner aspect of the cortex. Each bone sample was only attached to the testing setup by the screw threads with a block added to prevent rotation of the bone specimen (Figure 1a). The base plate for the jigs used an X-Y plate to allow perpendicular screw insertion.

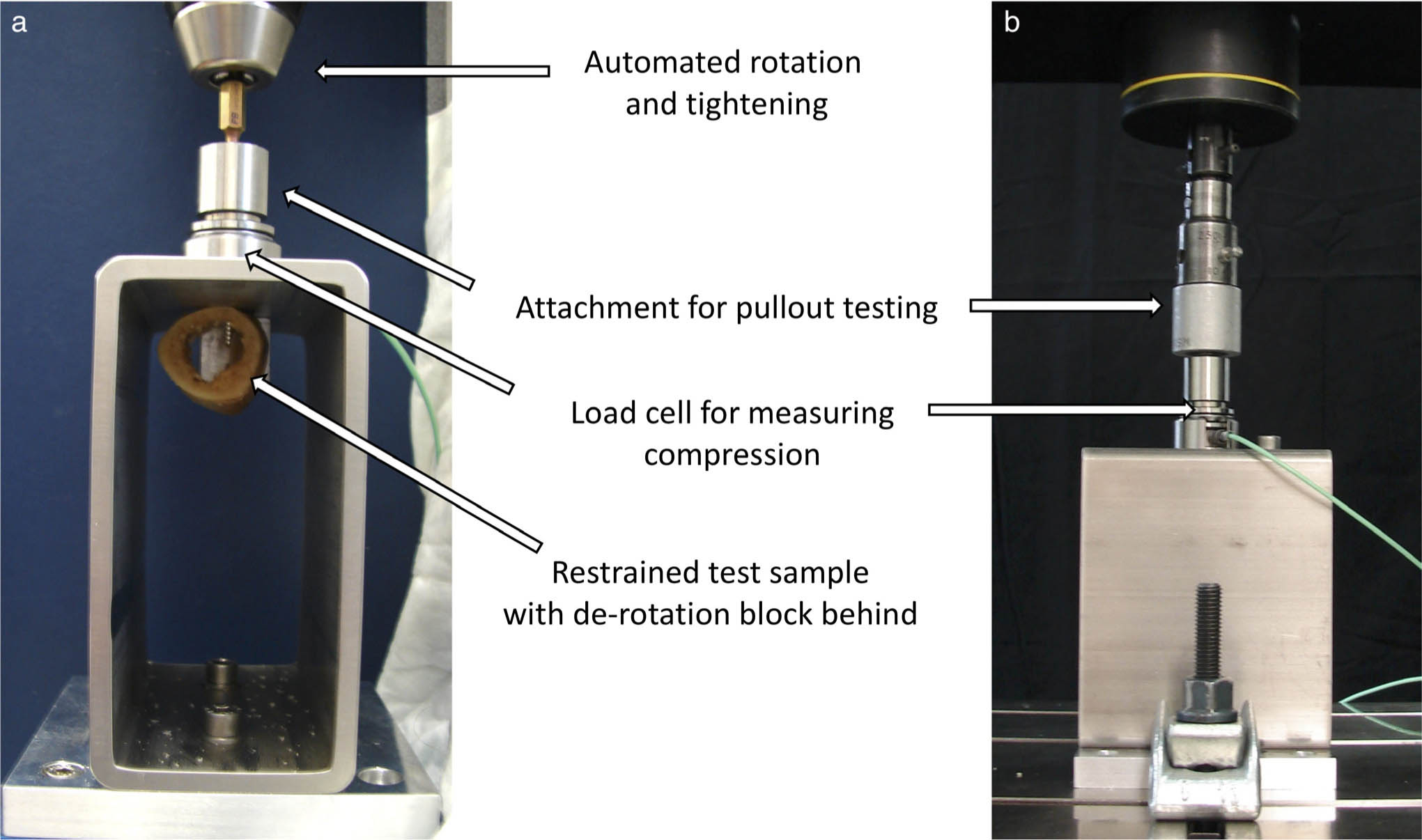
Fig. 1

a) Testing apparatus for automated insertion of screws with continuous compression recording. b) Material testing machine setup for pullout testing.

Using custom-made software (Matlab v2018b; The MathWorks, Natick, Massachusetts, USA), compression generated between the screw head and bone was recorded at 100 Hz. Constructs were mounted onto a material testing machine Instron 5943 (Instron, Norwood, Massachusetts, USA), which performed rotation of the screw at a constant rate of 7.5 revolutions per minute until stripping of the bone occurred (Figure 1a). Additionally, the torque was mean averaged over 60° of rotation prior to screw head contact against the jig and was chosen to represent T_plat. For the stripped samples, when the post stripping compression force had reached a plateau, the testing jig was removed and transferred to a second material testing machine Instron 5866 (Instron) for axial tensile testing (Figure 1b). The jigs used were designed to not disturb the fixation construct, as the superior attachment on the compression jig could be screwed into the load cell for axial pullout. The jig was attached to the actuator of the testing machine and axially loaded at a rate of 5 mm per minute,⁹ recording at 100 Hz until maximum force was observed. All force results were normalized according to cortical thickness.

Based on Equation 1, non-linear, least-squares data fitting (Matlab v2018b) was used to find the optimal values for the coefficient of friction and TYS; initial conditions were set to 0.4^11,12 and 90 MPa^11–13 respectively. Regions of the solution search were bound between 0 and 1 for f and between 1 MPa and 120 MPa for TYS. To validate these variables and Equation 1, half of the experimental stripping values were used to recalculate f and TYS. This version of Equation 1 was then used to predict T_str for the other ten samples.

Results

Cortical thickness demonstrated a linear relationship with experimental T_str (R² = 0.862; p < 0.001, simple linear regression) (Figure 2a). Compression reduced by approximately 95% when screw holes were stripped compared to unstripped insertions (mean post-stripping normalized compression of 11 N/mm (SD 7) (n = 20) compared to mean maximum normalized compression of 222 N/mm (SD 69) (n = 20)). The pullout force for stripped screw holes was reduced by 93% compared to unstripped insertions (mean 32 N/mm (SD 26) (n = 20) compared to mean maximum normalized pullout force 468 N/mm (SD 115) (n = 66)). To calibrate Equation 1, non-linear optimization based on half of the initial samples (n = 10) found a friction coefficient of 0.269 and TYS of 60.90 MPa. Using this version of Equation 1 to predict T_str for the other ten samples that were destructively tested showed a significant and meaningful correlation between predicted and experimental T_str (R² = 0.894; p < 0.001, simple linear regression) (Figure 2b).

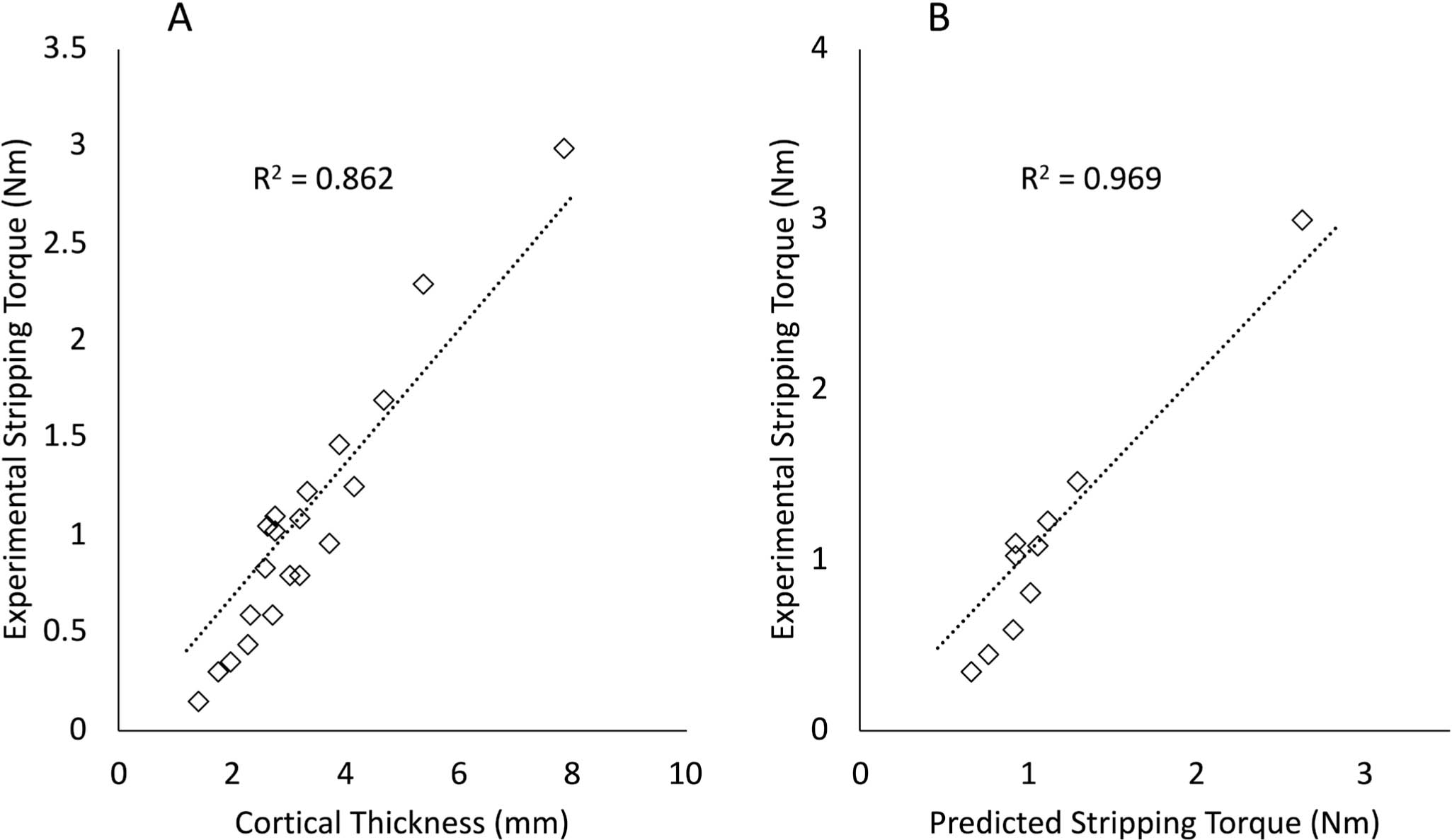
Fig. 2

a) Relationship between cortical thickness and experimental stripping torque (T_str) for 20 samples. b) Relationship between the predicted T_str calculated using Equation 1 and the experimental T_str for ten samples.

T_plat showed a relationship to experimental T_str of R² = 0.901 (p < 0.001, simple linear regression) (Figure 3), described by the following equation:

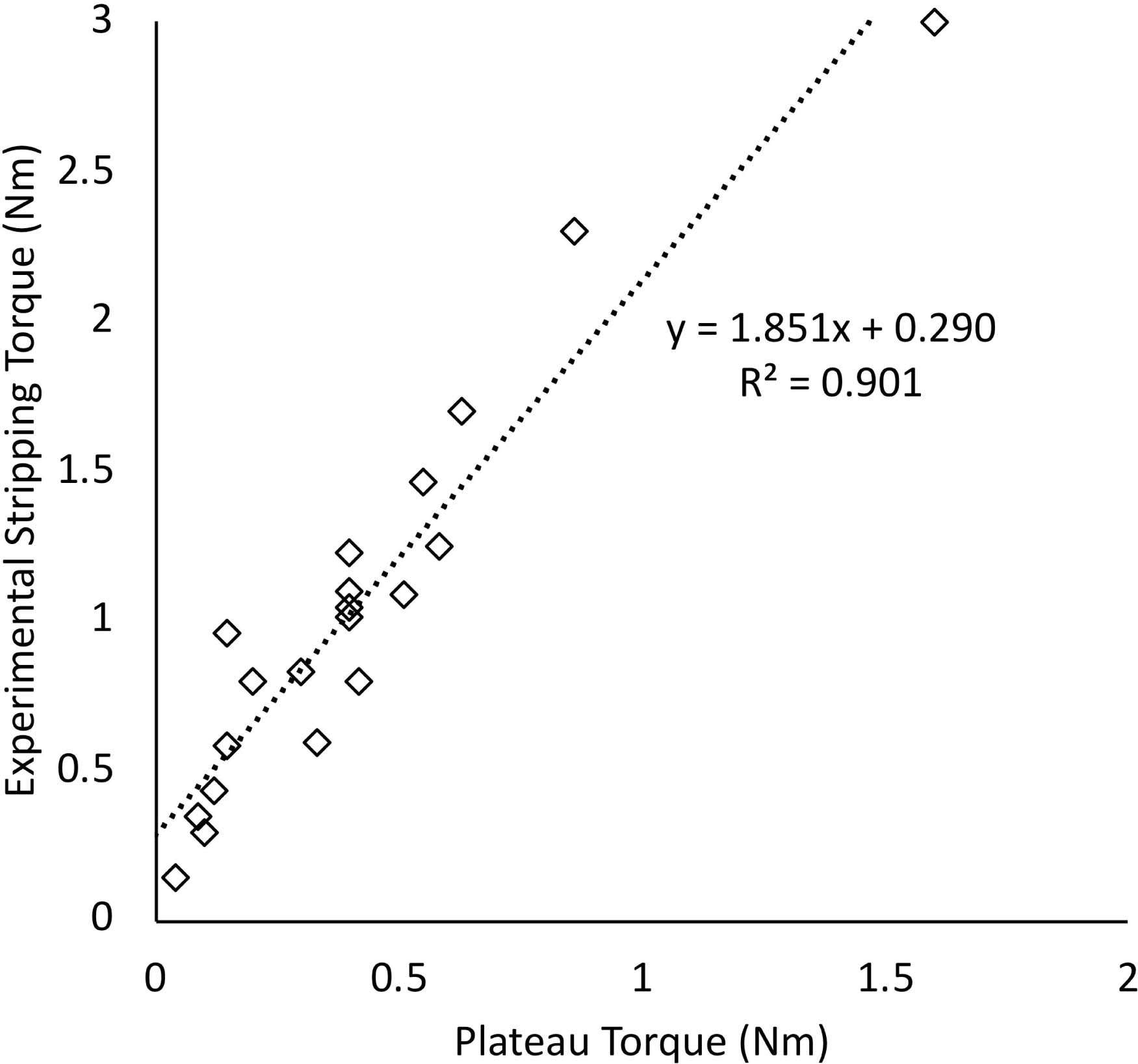
Fig. 3

Relationship between the plateau torque prior to screw head engagement and experimental stripping torque (n = 20).

When investigating optimum tightness, 4/66 samples (7%) were inadvertently stripped and excluded; statistical analysis was performed for the remaining 62 samples. When analyzing all unstripped data points, as tightness increased, compression increased (R² = 0.495; p < 0.001, simple linear regression). However, when tightness groupings were compared for changes in the relationship between tightness and compression, further increases in tightness from 75% to 85% and 75% to 95% did not generate any significant increases in compression (both p = 1.000, two-sided independent-samples t-test) (Figure 4). Normalized pullout forces did not show any change as tightness increased between 40% and 100% of T_str (R² = 0.014; p = 0.175, simple linear regression), though pullout forces at 95% tightness were non-significantly less (p = 0.060 to p = 0.655, two-sided independent-samples t-test) than at all other tightness percentages (Figure 5). Finally, cortical thickness was found to correlate with unnormalized pullout force (R² = 0.711; p < 0.001, simple linear regression).

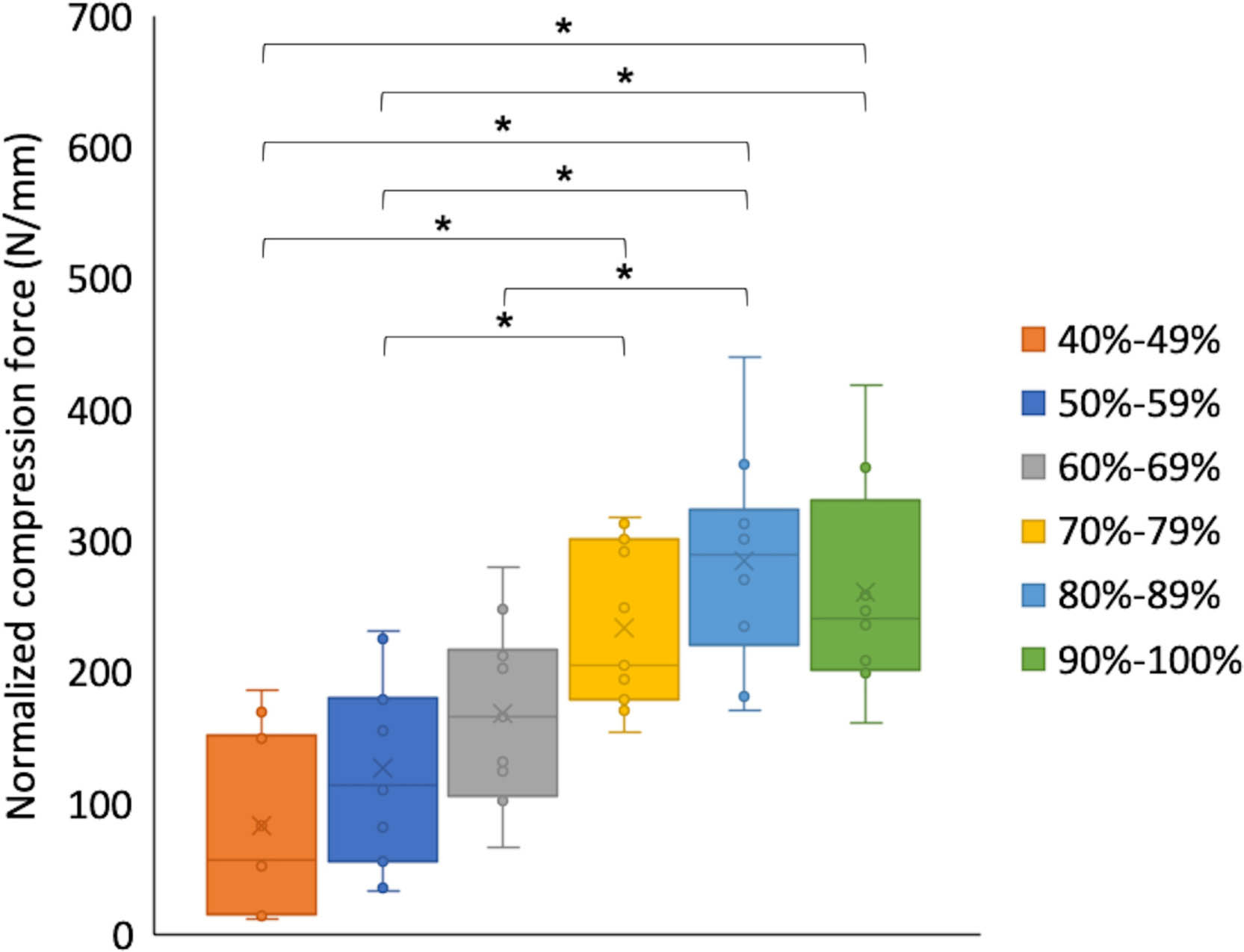
Fig. 4

Experimental values and box plot diagram of normalized compression force (N/mm) in decile groupings as functions of screw tightness (as a percentage of the stripping torque) (n = 62). *p < 0.05, two-sided independent-samples t-test.

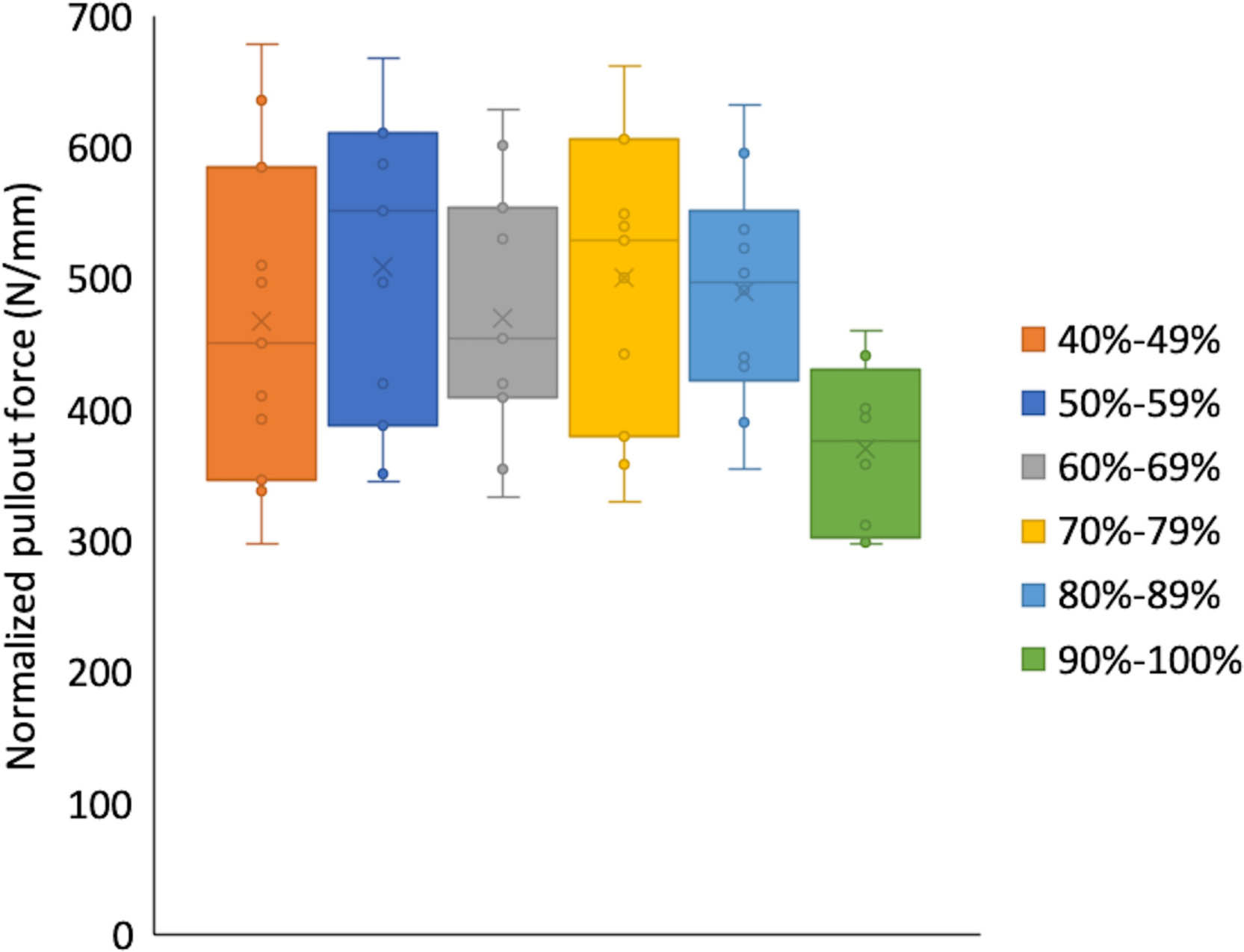
Fig. 5

Experimental values and box plot diagram of normalized pullout force (N/mm) in decile groupings as functions of screw tightness (as a percentage of the stripping torque) (n = 62).

Discussion

Maximum and optimum torques can be reliably calculated for cortical bone screw holes in human bone, being found between 70% and 80% of T_str. The hypothesis that submaximal torques prove optimal can be accepted.

With one in four non-locking screws stripping the surrounding material when manually inserted,² any methods for identification of torque limits should help address these failures of surgical technique. The primary goal with screw insertion should be to prevent stripping of the surrounding material, given that the compression and pullout forces reduce so dramatically if this occurs. Secondary objectives should include optimization of the screw-bone construct by achieving the greatest compression, and the greatest pullout resistance. Using calculations based on bone material properties should increase the chances of achieving the primary goal as the proprioceptively unpredictable stripping limit can be foreseen, preventing the irreversible damage and complications that occur if exceeded.

The findings from this study can be implemented into clinical practice in several ways. Firstly, they show that more tightness, beyond 80% of T_str, does not produce any additional benefits to the construct. This means that tightening to the maximum torque is inadvisable. Secondly, using estimates of TYS, even if these are only based on the cortical thickness and literature values for the friction coefficient and TYS, a targetable torque can be calculated preoperatively. This can reduce the chance of accidental stripping, which occurs all too commonly, especially in low-density bone and during training.² As low-energy fractures are likely to be associated with lower T_str due to lower TYS of the bone, lower coefficients of friction, and thinner cortices, using torque indicating screwdrivers that specify when predetermined torques are reached could reduce the risks of screws stripping the surrounding bone. This would be especially useful in situations where the stripping tightness is found well within the range of torques applicable by a surgeon; up to 2.0 Nm for 3.5 mm cortical screws.¹⁵

This study is the first to quantify optimum tightness in human cadaveric bone, and supports previous work using a bovine model that also demonstrated how exceeding 80% of T_str gave no benefit to constructs regarding compression and pullout force.⁷ Other studies in juvenile ovine bone demonstrated that tightening to 50% or 70% of T_str (determined based on stripping a screw in the contralateral tibia) resulted in no difference in pullout force, but there was a significant (p < 0.05) reduction from 70% to 90% of T_str.¹⁶ However, compression was removed prior to pullout and the results were limited by having only 20 samples distributed among the three tightness groups.

There were a number of study limitations. In biomechanical testing, especially when using human bone, controlling all variables can be difficult. By using automated screw insertion to a target tightness, variability due to manual insertion was removed. However, in vivo, manual tightening may generate different findings. During screw insertion in this study, even using controlled automated insertion, four samples (7%) stripped the bone, meaning that overestimation of T_str must have occurred in these cases; one when targeting 85% and three when targeting 95%. This is most likely to have arisen due to errors in measuring the cortical thickness and/or due to the heterogeneity of the cortical bone. This highlights that even under controlled laboratory conditions, overtightening still occurred when targeting high percentages of T_str – so may occur even more easily in less controlled operative environments. Given that no benefits could be seen in tightening beyond 80%, and that errors might occur in achieving 80% of the theoretical T_str in vivo (due to inaccuracies in measuring bone properties), the case is strengthened for remaining in a safe torque range (between 70% and 80% of the maximum), away from the stripping limit.

The bone used was assumed as a homogeneous material to enable the predictions to be made. While using the specimen of just one donor will have reduced the variability in bone characteristics, TYS and coefficient of friction are likely to have varied between screw holes. Furthermore, as no direct measurement of the bone density was performed, these findings may not represent all bone types surgically encountered. It may be that the tightness beyond which there is no further benefit increases with denser bone – further studies using different densities are needed to establish this. Other materials such as titanium behave differently to stainless steel screws in fracture fixation¹⁷ – the optimum tightness in other metals may be different to those in this study. Several variables within the study were at risk of error, such as the cortical thickness measured and the perpendicularity of the screw holes. Although, as one researcher (JWAF) performed all sample preparations and screw insertions, interoperator errors will have been eliminated. While several other variables were controlled by using the same screw geometries each time, further work will be needed to validate these methods using different screw shapes and sizes, and in different regions of human bones. All screws were inserted only unicortically to ensure perpendicular orientation to the cortex, thus the findings may require validation in bicortical samples. However, it has been shown that splitting cortical thickness into a near and far cortex, rather than a single cortex of the same total thickness, does not seem to affect the relationship between cortical thickness and applied forces.^18–20 Finally, the pullout testing methods used are only an assessment of the immediate implantation consequences and offer no assessment of healing effects, or of changes in constructs as stress dissipates over time and under loading. Future work will be required to implement methods for optimizing fixation torques and measuring the clinical impacts from this.

Predictions of T_str based on screw geometries and bone characteristics enable preinsertion calculation of the optimum torque, found to be between 70% and 80% of the maximum. Further tightening once the screw head has made contact does not generate greater pullout forces, however it increases the risk of stripping the surrounding bone – associated with reductions in compression and pullout force of more than 90%. Following further investigation using different screw geometries and considering the effect of bone healing, these findings can be incorporated into screw fixation strategies to ensure optimum torque is achieved intraoperatively.