Abstract
Objectives
Because of the contradictory body of evidence related to the potential benefits of helical blades in trochanteric fracture fixation, we studied the effect of bone compaction resulting from the insertion of a proximal femoral nail anti-rotation (PFNA).
Methods
We developed a subject-specific computational model of a trochanteric fracture (31-A2 in the AO classification) with lack of medial support and varied the bone density to account for variability in bone properties among hip fracture patients.
Results
We show that for a bone density corresponding to 100% of the bone density of the cadaveric femur, there does not seem to be any advantage in using a PFNA with respect to the risk of blade cut-out. On the other hand, in a more osteoporotic femoral head characterised by a density corresponding to 75% of the initial bone density, local bone compaction around the helical blade provides additional bone purchase, thereby decreasing the risk of cut-out, as quantified by the volume of bone susceptible to yielding.
Conclusions
Our findings indicate benefits of using a PFNA over an intramedullary nail with a conventional lag screw and suggest that any clinical trial reporting surgical outcomes regarding the use of helical blades should include a measure of the femoral head bone density as a covariable.
Article focus
This computational study aims to assess the role of bone compaction with respect to implant cut-out using a CT-scan based finite element model of trochanteric fractures
Key messages
Bone compaction decreases the risk of cut-out when the head is very osteoporotic (mean Young’s modulus of 533 MPa) but is moot for higher bone densities (Young’s modulus of 820 MPa)
Strengths and limitations
This is the first computational study to include bone compaction in a finite element model of fracture fixation with helical blades and supplements the contradictory body of evidence from in vitro experimental studies on potential benefits of the PFNA
This study provides a clinically useful conclusion regarding the relative merit of stabilising trochanteric fractures with a PFNA depending on femoral head bone density in the patient
A possible limitation of this study is the use of a single bone specimen, making our study subject-specific. In order to address this limitation, we varied the mean bone density of the cadaveric bone to model osteoporosis
Introduction
Cut-out is the major cause of implant failure in the fixation of trochanteric fractures, accounting for more than 80% of failures in cases using dynamic hip screws (DHSs).1 The rate of cut-out reported for intramedullary devices can be as high as 8%.1 There has been an increasing interest in evaluating the efficacy of helical blades in decreasing this risk. The insertion of a helical blade without reaming leads to bone compaction. In fact, an imaging study quantified this increase in bone density, and concluded that the density of trabecular bone increased by up to 30% in an appropriately sized cylinder surrounding the helical blade of a DHS blade.2
However the different biomechanical studies published so far do not seem to agree on whether this compaction effectively leads to better implant anchorage. O’Neill et al3 concluded that the DHS blade is superior to a conventional DHS in terms of cut-out resistance, mainly by using polyurethane foam blocks.3 Wähnert et al4 did not find any difference in resistance to cut-out when comparing cadaveric femora instrumented with a DHS blade with or without pre-drilling. Born et al5 even reported a better migration resistance for conventional screws when compared with helical blades anchored in polyurethane foam blocks. Since the current body of evidence spans the whole spectrum from worse to better and since all these engineering studies are experimental and not computational, we thought it would be useful to design a finite element study to assess whether local bone compaction had an effect on cut-out resistance.
Furthermore, none of the biomechanical studies published so far consider a clinically relevant trochanteric fracture type with lack of medial support and most of them are not specifically dealing with the PFNA, but rather with the DHS blade, which has different biomechanics. They either use an isolated femoral head or foam blocks3,5 or femora with no medial fragment removed.4 Yet, we have proven using finite element analysis (data to be published soon) the importance of taking into account the size of the medial fragment, which we will refer to as the intrusion distance.
It is therefore the aim of this study to assess the influence of bone compaction on blade cut-out, using a subject-specific finite element (FE) model of a clinically relevant trochanteric fracture stabilised with a PFNA. We hypothesise that bone compaction contributes to a decrease in the risk of cut-out only when the head is very osteoporotic.
Materials and Methods
A medial wedge of 10° was removed from the femur of a female cadaver (aged 78 years at death with weight of 64 kg and body mass index of 21.9 kg/m2) to model a three-part peritrochanteric fracture (31-A2, AO classification6). The angle of the fracture line with the shaft of the femur was assigned a value of 43° and the intrusion distance into the fracture complex was assumed to be 60% (Fig. 1). The CT scan of the femur was converted to a mixed hexahedral/tetrahedral mesh with Simpleware software suite (Simpleware Ltd, Exeter, United Kingdom) and imported into an FE solver (Abaqus; Simulia, Providence, Rhode Island).
![Fig. 1
Diagram showing the calculation
of the intrusion distance of the medial fragment into the fracture
complex: defined as the ratio of the length of the medial wedge
in the anteroposterior view (AB) to the length of the fracture line
(AC) and expressed as a percentage ([AB/AC] × 100).](/api/asset/2046-3758.25.2000150/2000150-galleyfig1.jpeg)
Fig. 1
Diagram showing the calculation of the intrusion distance of the medial fragment into the fracture complex: defined as the ratio of the length of the medial wedge in the anteroposterior view (AB) to the length of the fracture line (AC) and expressed as a percentage ([AB/AC] × 100).
A linear relationship between Hounsfield units and ash density was assumed, and we chose the following density–elasticity relationship to convert apparent density (ρ, in g/cm3) into Young’s modulus (E, in MPa)7: E = 6950ρ1.49. Ash density was assumed to be 60% of apparent density.8Table I gives properties of the femoral head in terms of quantitative CT bone mineral density (BMD) and mean Young’s modulus calculated according to the aforementioned density–elasticity relationship. Bone was assigned a value of 0.3 for Poisson’s ratio. Bone compaction was modeled as a 30% increase in bone density in a cylinder around the helical blade (14 mm diameter).2
Table I
Donor data
| Femoral head parameters | Mean bone mineral density | Mean Young’s modulus |
|---|---|---|
| 75% bone density | 107 mg/cm3 | 533 MPa |
| 100% bone density | 143 mg/cm3 | 820 MPa |
The PFNA (Synthes, Solothurn, Switzerland) with a length of 200 mm and angle of 125° was assigned a value of 105 GPa for Young’s modulus and 0.35 for Poisson’s ratio to model the mechanical properties of a titanium alloy. Frictional contact interactions were assumed between the different parts of the models. For the friction coefficients we took 0.46 for bone-bone interactions, 0.3 for bone-implant interactions and 0.23 for implant-implant interactions.9
The FE models were subjected to a load of 1866 N corresponding to the maximal loading on the hip during a walking cycle for a person with a weight of 80 kg.10 This is a common loading case scenario occurring during the recovery of patients after total hip replacement.9,11 The femoral head was constrained in the plane orthogonal to the loading vector while the distal end of the femur was constrained in all translational degrees of freedom at a point located in the mid-coronal plane, at 23 mm medially from the shaft axis. The femur was able to rotate about this pivotal point about the frontal and the sagittal axis.
Results
In order to characterise failure of the PFNA by cut-out, it is necessary to consider compressive strains in the region superior to the helical blade. For this purpose, contour plots showing minimum principal strains in a cross-section through the femoral head and neck are shown in Figure 2. We took -0.9% as the cut-off value (yield strain) below which trabecular bone is susceptible to yielding (undergo irreversible deformations) in agreement with experimental results on trabecular bone.12,13 Areas featuring smaller minimum principal strains, i.e more compressive, than this threshold value were assigned a grey colour to emphasise the volume of bone susceptible to yielding and as a consequence likely to be involved in failure of the osteosynthesis.
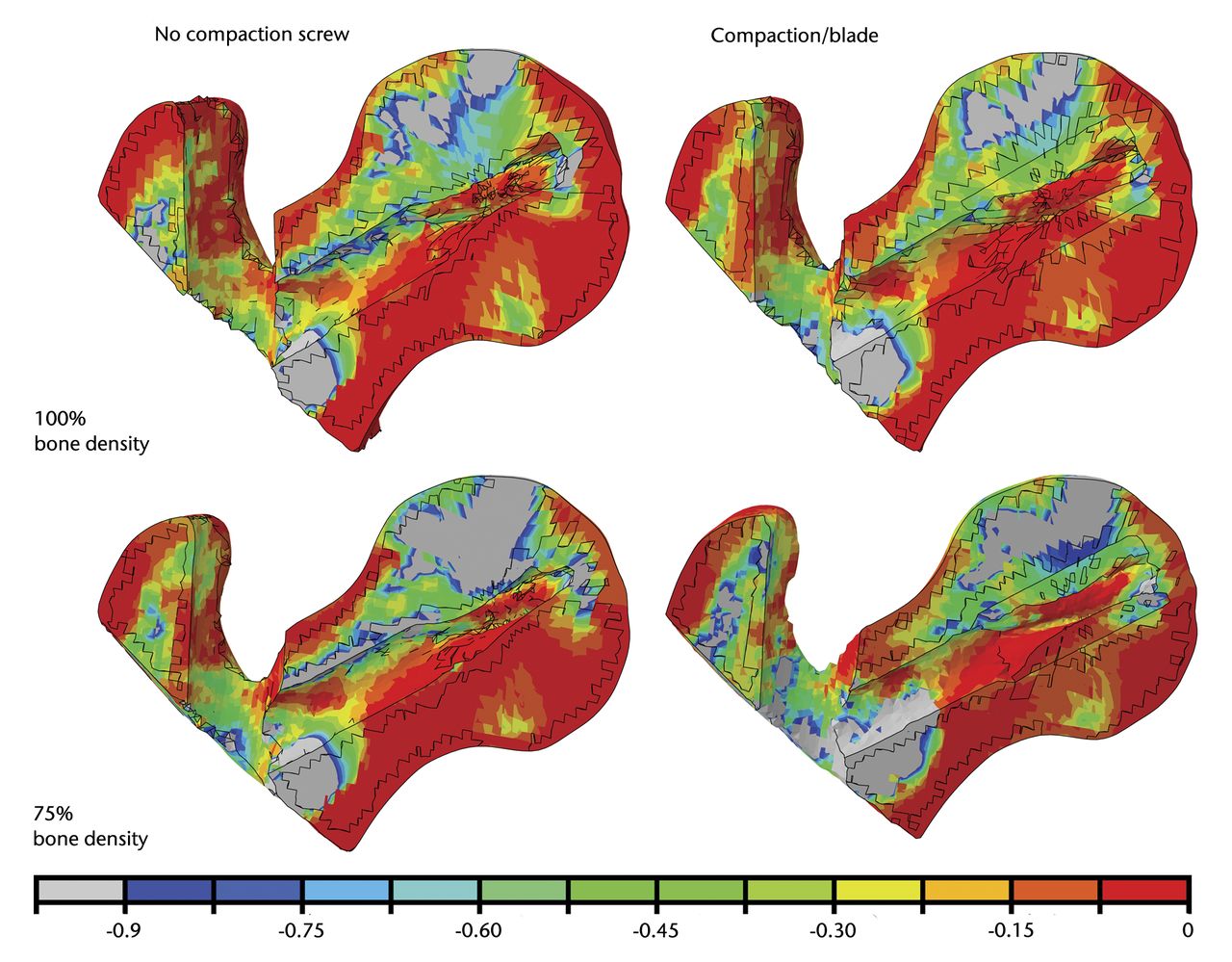
Fig. 2
Diagrams showing the minimum (compressive) principal strains plotted in percent with a yield strain cut-off value of -0.9%. Grey regions have strains below -0.9% and are at higher risk of being involved in blade cut-out.
Contour plots show that for a bone density corresponding to 100% of the cadaveric bone density, the bone area immediately superior to the top of the helical blade does not fall beyond the yield strain cut-off value neither for the case without compaction nor for the case with bone compaction around the helical blade. On the other hand, for a bone with 75% of the density of the cadaveric bone used in this study, contour plots show that trabecular bone undergoes more compressive strains than our threshold value if compaction is not modelled. When local bone compaction around the helical blade is modelled, the bone area immediately superior to the helical blade shows no susceptibility to yielding. The general trends that can be observed on the contour plots were confirmed by quantifying the volume of bone susceptible to yielding, i.e. volume of the region (in the femoral head) featuring minimum principal strains more compressive than a yield strain of -0.9% (Fig. 3).
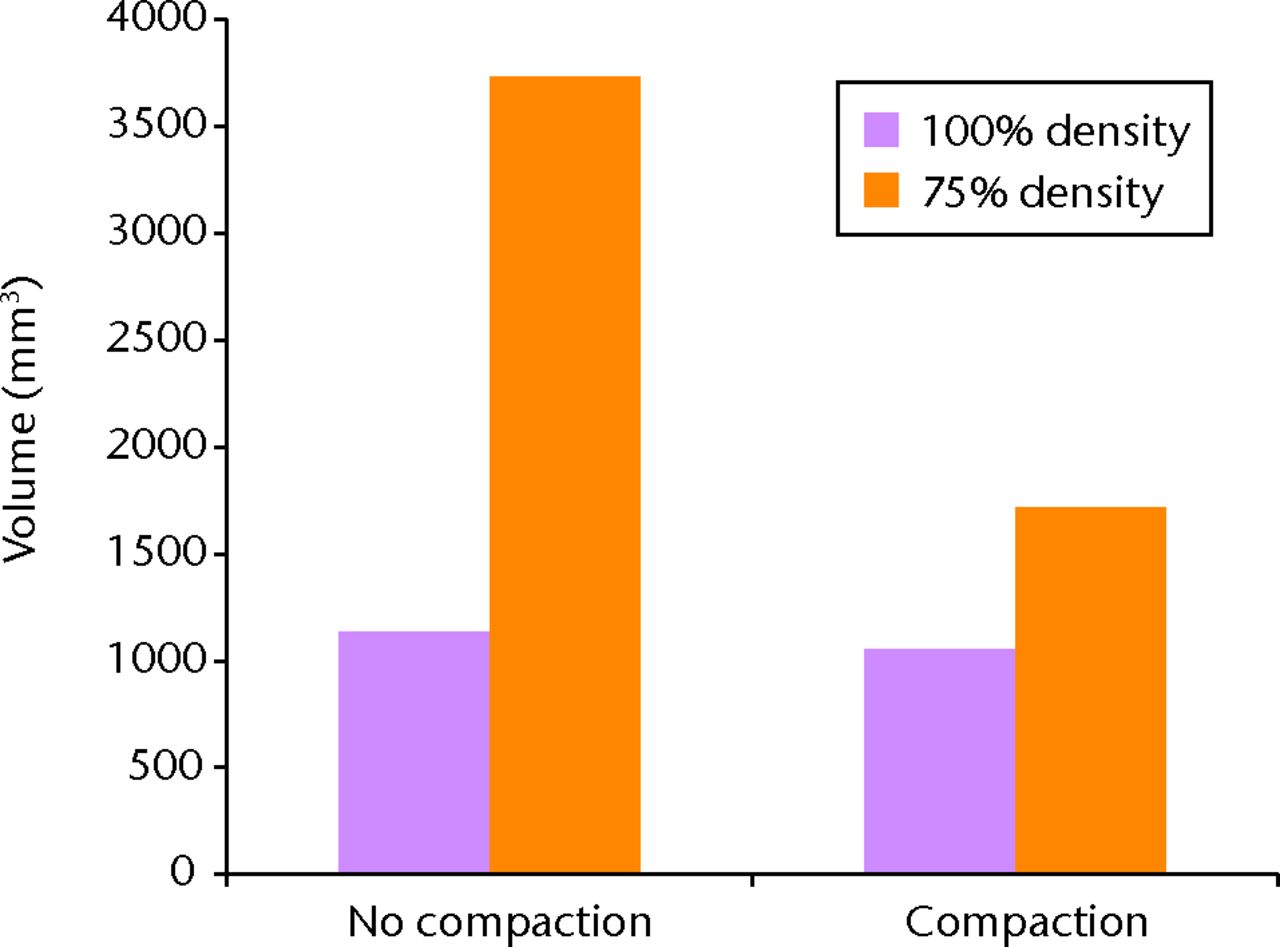
Fig. 3
Bar chart showing the volume of bone susceptible to yielding calculated by using a yield strain cut-off value of -0.9% for minimum principal strains. The higher this volume, the greater the risk of blade cut-out.
Discussion
A recent imaging study14 quantified femoral head bone density in hip fracture patients and compared it with a fracture-free control group with a similar age range. The authors showed that the mean femoral head density in the hip fracture group was 75% of the femoral head density in the fracture free group. We therefore considered that taking the CT scan of a healthy cadaveric bone, even when harvested from an old donor, could be misleading and this led us to analyse our finite element models with 100% and 75% of the bone density of the cadaveric bone. According to that study, Table I shows that 100% (respectively 75%) of the average bone density of the femoral head in our FE models correspond to the mean value (182 mg/cm3) minus 1 (respectively 2) standard deviation(s) of data obtained on hip fracture patients. Our low density models can therefore be considered to be adequate to illustrate severe osteoporosis in elderly patients.
From the observation of contour plots, it seems that for a density corresponding to 100% of the density of the cadaveric bone used in this study, the local trabecular bone compaction does not have much impact on implant anchorage because the bone density around the helical blade is already sufficient to provide adequate bone purchase. In other words, the use of a PFNA in this case does not seem to be superior to a conventional intramedullary nail. On the other hand, a more osteoporotic femoral head with a bone density corresponding to 75% illustrates a case where the use of a helical blade such as the PFNA could decrease the risk of cut-out. In fact, the contour plots show that a bone region around the helical blade is not susceptible to yielding when compaction is taken into account while a similar model without bone compaction seems to predict cut-out.
Quantification of the volume of bone susceptible to yielding in the head of each of the four models confirms the conclusions drawn from the contour plots (Fig. 3) and clearly labels the low density (75%) model without compaction as the model at high risk of cut-out, compared to the three others. This suggests that using intramedullary blade implants could actually compensate for the poor bone density of severely osteoporotic patients by providing additional mechanical support to the implant in the femoral head and therefore lowers the risk of cut-out down to a level comparable to the one found in a bone with a much higher average bone density (FE model with 100% of the bone density).
For all our models, the helical blade was positioned centrally in the femoral head both in AP and lateral views as recommended by Zhou et al.15 Tip-apex distance was within the acceptable range. The authors of this letter reported more than 500 PFNA cases without any cut-out or medial perforation, thereby confirming on a larger scale the promising lack of cut-out cases in our department of orthopaedic surgery in Luxembourg. However clinical studies attempting to compare screw versus blade have been published and the conclusions are not so obvious. First, Mereddy et al16 reported a cut-out rate with the PFNA of 3.6% while Simmermacher et al17 published a cut-out rate of 2.3%, both of which did not compare it with conventional lag screws. A study led by Yaozeng et al18 then compared the Gamma nail with the PFNA without being able to find any significant differences in terms of treatment outcome. Another study compared screw versus helical blade but pooled sliding hip screw cases together with Gamma nail cases in the screw group and DHS blade with PFNA in the blade group.19 They reported a cut-out rate of 1.5% for the blade group compared with 2.9% for the screw group. However, it is difficult to draw meaningful conclusions from this study because the absolute number of cut-out cases is probably too small.
Linear elasticity, combined with a minimum principal strain criterion to predict an increased risk of failure by cut-out, is an adequate computational model to support our results within the scope of this study.20 The density–elasticity relationship of trabecular bone used in this study was established for intact trabecular bone. It is however reasonable to use it as well to model the behaviour of compacted trabecular bone. Indeed, as reported by Windolf et al,2 the increase in density characterising bone compaction around a helical blade is mostly due to elastic deformation of the trabeculae. The visco-elastic ‘spring-back’ effect of trabecular bone was demonstrated in that experimental study by quantifying the relaxation of the bone structure following removal of the helical blade, confirming the hypothesis that the trabeculae are deformed in the elastic range.
A constant increase in bone density was used to model compaction since it was shown that compaction following insertion of a helical blade was independent of the initial bone mineral density.2 It is not appropriate to study the effect of bone compaction separately from using the helical blade design. It was indeed shown that conventional screw threads do not exhibit this ability to compact bone in their vicinity.21 The bone density was actually shown to be lower around a dynamic hip screw compared to the contralateral side.
Finally, regarding the use of a single bone specimen, similar results would be obtained with data from other bone samples if the average density of the femoral head fell in the range of densities used in this study (107 mg/cm3 to 143 mg/cm3).
Conclusions
Our FE models show that only when the femoral head bone density is low, there is an advantage in using a helical blade to provide better bone purchase. This superiority of the PFNA is relinquished for the model with 100% of the bone density. We therefore conclude that the PFNA has the potential to decrease the number of cut-out cases in severely osteoporotic patients and we recommend including the bone density of the femoral head as a covariable in any clinical trial devoted to helical blade implants in order to confirm the surgical indications for the use of such implants.
Synthes GmbH (Solothurn, Switzerland) is acknowledged for the provision of CAD models of the PFNA. The first author was supported by a Principal’s Career Development Scholarship awarded by The University of Edinburgh and by a scholarship awarded by Centre Hospitalier de Luxembourg.
1 Lorich DG , GellerDS, NielsonJH. Osteoporotic pertrochanteric hip fractures: management and current controversies. Instr Course Lect2004;53:441–454.PubMed Google Scholar
2 Windolf M , MuthsR, BraunsteinV, et al.Quantification of cancellous bone-compaction due to DHS Blade insertion and influence upon cut-out resistance. Clin Biomech (Bristol, Avon)2009;24:53–58.CrossrefPubMed Google Scholar
3 O’Neill F , CondonF, McGloughlinT, et al.Dynamic hip screw versus DHS blade: a biomechanical comparison of the fixation achieved by each implant in bone. J Bone Joint Surg [Br]2011;93-B:616–621.CrossrefPubMed Google Scholar
4 Wähnert D , GudushauriP, SchiumaD, RichardsG, WindolfM. Does cancellous bone compaction due to insertion of a blade implant influence the cut-out resistance?: a biomechanical study. Clin Biomech (Bristol, Avon)2010;25:1053–1057. Google Scholar
5 Born CT , KarichB, BauerC, von OldenburgG, AugatP. Hip screw migration testing: first results for hip screws and helical blades utilizing a new oscillating test method. J Orthop Res2011;29:760–766.CrossrefPubMed Google Scholar
6 No authors listed. Fracture and dislocation compendium: Orthopaedic Trauma Association Committee for Coding and Classification J Orthop Trauma1996;10(Suppl 1):1–154. Google Scholar
7 Schileo E , TaddeiF, MalandrinoA, CristofoliniL, VicecontiM. Subject-specific finite element models can accurately predict strain levels in long bones. J Biomech2007;40:2982–2989.CrossrefPubMed Google Scholar
8 Schileo E , Dall’araE, TaddeiF, et al.An accurate estimation of bone density improves the accuracy of subject-specific finite element models. J Biomech2008;41:2483–2491.CrossrefPubMed Google Scholar
9 Eberle S , GerberC, von OldenburgG, HögelF, AugatP. A biomechanical evaluation of orthopaedic implants for hip fractures by finite element analysis and in-vitro tests. Proc Inst Mech Eng H2010;224:1141–1152.CrossrefPubMed Google Scholar
10 Bergmann G , DeuretzbacherG, HellerM, et al.Hip contact forces and gait patterns from routine activities. J Biomech2001;34:859–871.CrossrefPubMed Google Scholar
11 Morlock M , SchneiderE, BluhmA, et al.Duration and frequency of every day activities in total hip patients. J Biomech2001;34:873–881.CrossrefPubMed Google Scholar
12 Kopperdahl DL , KeavenyTM. Yield strain behavior of trabecular bone. J Biomech1998;31:601–608.CrossrefPubMed Google Scholar
13 Bevill G , FarhamandF, KeavenyTM. Heterogeneity of yield strain in low-density versus high-density human trabecular bone. J Biomech2009;42:2165–2170.CrossrefPubMed Google Scholar
14 Bousson VD , AdamsJ, EngelkeK, et al.In vivo discrimination of hip fracture with quantitative computed tomography: results from the prospective European Femur Fracture Study (EFFECT). J Bone Miner Res2011;26:881–893.CrossrefPubMed Google Scholar
15 Zhou JQ , ChangSM. Failure of PFNA: helical blade perforation and tip-apex distance. Injury2012;43:1227–1228.CrossrefPubMed Google Scholar
16 Mereddy P , KamathS, RamakrishnanM, MalikH, DonnachieN. The AO/ASIF proximal femoral nail antirotation (PFNA): a new design for the treatment of unstable proximal femoral fractures. Injury2009;40:428–432.CrossrefPubMed Google Scholar
17 Simmermacher RK , LjungqvistJ, BailH, et al.The new proximal femoral nail antirotation (PFNA) in daily practice: results of a multicentre clinical study. Injury2008;39:932–939.CrossrefPubMed Google Scholar
18 Yaozeng X , DechunG, HuilinY, GuangmingZ, XianbinW. Comparative study of trochanteric fracture treated with the proximal femoral nail anti-rotation and the third generation of gamma nail. Injury2010;41:1234–1238.CrossrefPubMed Google Scholar
19 Stern R , LubbekeA, SuvaD, MiozzariH, HoffmeyerP. Prospective randomised study comparing screw versus helical blade in the treatment of low-energy trochanteric fractures. Int Orthop2011;35:1855–1861.CrossrefPubMed Google Scholar
20 Schileo E , TaddeiF, CristofoliniL, VicecontiM. Subject-specific finite element models implementing a maximum principal strain criterion are able to estimate failure risk and fracture location on human femurs tested in vitro. J Biomech2008;41:356–367.CrossrefPubMed Google Scholar
21 Steinberg EL , SternheimA, BlacharA. Femoral head density on CT scans of patients following hip fracture fixation by expandable proximal peg or dynamic screw. Injury2010;41:647–651. Google Scholar
Funding statement:
None declared
Author contributions:
J. M. Goffin: Design of project, Data collection and analysis, Writing of paper
P. Pankaj: Modelling methodologies, Analysis of results, Paper writing support
A. H. R. W. Simpson: Discussion/design of project, Writing of paper
R. Seil: Discussion/design of project, Writing of paper
T. G. Gerich: Discussion/design of project, Writing of paper
ICMJE Conflict of Interest:
None declared
©2013 The British Editorial Society of Bone & Joint Surgery. This is an open-access article distributed under the terms of the Creative Commons Attributions licence, which permits unrestricted use, distribution, and reproduction in any medium, but not for commercial gain, provided the original author and source are credited.










