Abstract
Objectives
This study aims to assess the correlation of CT-based structural rigidity analysis with mechanically determined axial rigidity in normal and metabolically diseased rat bone.
Methods
A total of 30 rats were divided equally into normal, ovariectomized, and partially nephrectomized groups. Cortical and trabecular bone segments from each animal underwent micro-CT to assess their average and minimum axial rigidities using structural rigidity analysis. Following imaging, all specimens were subjected to uniaxial compression and assessment of mechanically-derived axial rigidity.
Results
The average structural rigidity-based axial rigidity was well correlated with the average mechanically-derived axial rigidity results (R2 = 0.74). This correlation improved significantly (p < 0.0001) when the CT-based Structural Rigidity Analysis (CTRA) minimum axial rigidity was correlated to the mechanically-derived minimum axial rigidity results (R2 = 0.84). Tests of slopes in the mixed model regression analysis indicated a significantly steeper slope for the average axial rigidity compared with the minimum axial rigidity (p = 0.028) and a significant difference in the intercepts (p = 0.022). The CTRA average and minimum axial rigidities were correlated with the mechanically-derived average and minimum axial rigidities using paired t-test analysis (p = 0.37 and p = 0.18, respectively).
Conclusions
In summary, the results of this study suggest that structural rigidity analysis of micro-CT data can be used to accurately and quantitatively measure the axial rigidity of bones with metabolic pathologies in an experimental rat model. It appears that minimum axial rigidity is a better model for measuring bone rigidity than average axial rigidity.
Article focus
-
Use of CT-based Structural Rigidity Analysis to assess the average and minimum axial rigidities of cortical and trabecular femur segments from normal, ovariectomised, and partially nephrectomised rats
-
Comparing the results to mechanical testing as the gold standard measure
Key messages
-
Despite continued development of new therapies and treatments to prevent and treat fragility fractures, accurate, non-invasive assessment of fracture risk remains an elusive task
-
Results of this study support thehypothesis that axial rigidity of bones with metabolic pathologies can be accurately and quantitatively assessed in a rat model by conducting structural rigidity analysis
-
Axial rigidity measured non-invasively by micro-CT was well correlated with the results from mechanical testing as the gold standard measure
Strengths and limitations of this study
-
Strength: animal study – where disease models are well controlled and mechanical testing can be conducted to confirm results
-
Limitation: animal study – further work in human beings must be conducted to assess human validity of this work
Introduction
Fragility fractures of the hip, spine or wrist resulting from osteoporosis and other bone diseases are common causes of disability, affecting up to 2 million Americans annually.1 While osteoporosis is assumed to be the cause of most fragility fractures, 25-OH-vitamin D deficiency is observed in 50% of postmenopausal women in the population who fracture their hip (not including those residing in retirement homes) and have no other cause for low bone mass.2 Vitamin D deficiency can result in osteomalacia, a bone material problem which has been diagnosed histologically (hypo-mineralized osteoid) in between 13% and 33% of patients with hip fractures.3
Moreover, secondary hyperparathyroidism, as seen in patients with renal disease, can cause demineralization of both the cortical and trabecular bones and can increase the risk of fracture by compromising the material properties of bone.4 Currently, the World Health Organization (WHO) uses decreased bone mineral density (BMD), as measured by dual energy X-ray absorptiometry (DXA), in order to identify patients with osteoporosis and osteopenia in order to identify individuals at risk for fragility fracture.5 However, BMD, an areal projection, is not a true measure of bone density and has shown to be neither sensitive nor specific in its ability to predict future fragility fracture.6
The strength of bone is determined by its material composition and structural organisation. DXA measurements are based on the areal projection of a two-dimensional construct, where trabecular and cortical bone components are integrated. In contrast, quantitative CT-based Structural Rigidity Analysis (CTRA),7-9 a three-dimensional imaging modality, can provide information about specific changes in bone material and structure for both cortical and trabecular bone. While DXA fails to distinguish changes in the composition of bone tissue from those changes occurring at the structural level, CTRA is capable of non-invasive assessment of axial, bending and torsional rigidities of bones from their trans-axial cross-sectional images. With this technique, modulus of elasticity (Young’s modulus) is treated as a function of bone density, and bone geometry is represented by its cross-sectional area and moment of inertia. While CTRA has been used extensively to assess fracture in studies of metastatic musculoskeletal lesions,7-9 efforts have not been made to assess the efficacy of this technique in assessing fracture risk in metabolic musculoskeletal diseases.
The ovariectomized (OVX) rat model has been widely used to study the effects of menopause on bone mass, trabecular microstructure and fracture risk10; and the partially nephrectomized (NFR) rat model has been used effectively to study the effects of renal osteodystrophy manifested as secondary hyperparathyroidism on bone metabolism.11 We have previously used the established ovariectomy model as a surrogate for an altered skeletal state in conjunction with the nephrectomy-induced renal osteodystrophy model and have demonstrated the deficiencies of DXA compared with quantitative computed tomography in detecting changes in trabecular bone microstructure in relation to changes in their mechanical properties.12 Our group has also described the relationships between the mechanical properties of normal, ovariectomized, and partially nephrectomized rat cortical and trabecular bone based on its mineral density, bone volume fraction and apparent density.13
Given the ability of CTRA to detect structural and material changes within trabecular and cortical bone, we hypothesised that CTRA can accurately assess the average and minimum axial rigidities of cortical and cancellous bones affected by metabolic diseases. To that end, we used CTRA to assess the average and minimum axial rigidities of cortical and trabecular femur segments from normal, ovariectomized and partially nephrectomized rats, and compared the results with those obtained from mechanical testing as the gold standard measure.
Materials and Methods
Animal model
A total of 30 female Sprague Dawley rats (around 15 weeks of age, weighing between 250 g and 275 g) were obtained and divided into three equally sized groups: the animals in the control group (n = 10) were not subjected to any surgical or dietary interventions; the OVX group (n = 10) underwent ovariectomy a week prior to the start of the study in order to induce a state of low bone mass and micro-architectural deterioration10,13; and the NFR group (n = 10) underwent 5/6 nephrectomy11,14 one week prior to the start of the study, in addition to being placed on a modified diet containing 0.6% Ca and 1.2% P for the duration of the study in order to induce renal osteodystrophy (normal rodent diet contains 1.35% Ca and 1.04% P) and severe secondary hyperparathyroidism.10,13 Both surgical procedures were conducted at the animal supplier facility one week prior to the arrival of the animals at the laboratory. The control, NFR and OVX animals were killed by CO2 inhalation four months after they arrived at our laboratory, in order to allow appropriate time for the onset and progression of diseases. The femurs from each animal were excised and used for the study (Fig. 1). The study protocol was approved by Beth Israel Deaconess Medical Center’s Institutional Animal Care and Use Committee.
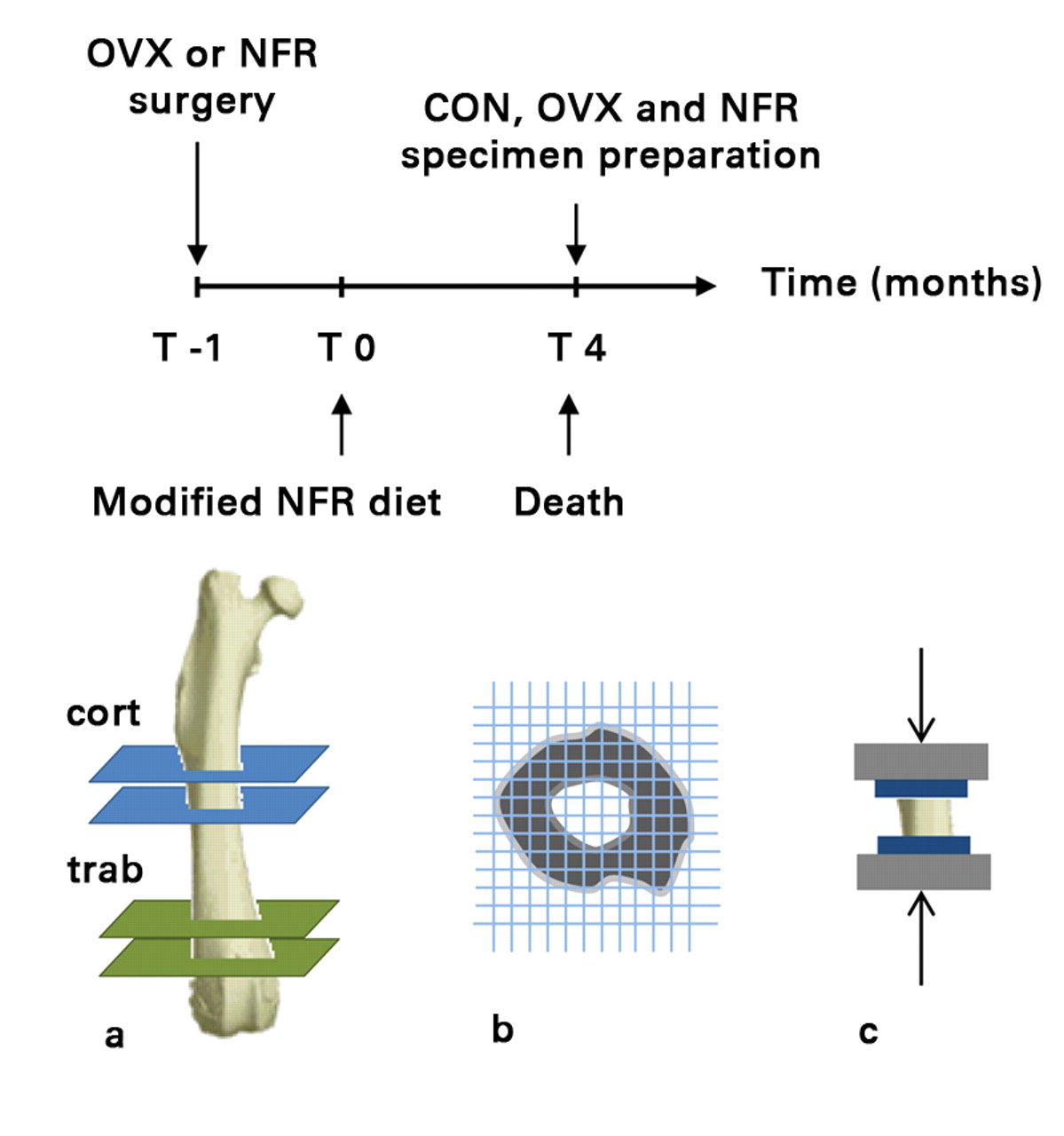
Fig. 1
Timeline followed prior to collection of specimens (top) and diagrams showing a) the mid-diaphyseal (cortical) and distal metaphyseal (trabecular) sections cut from each femur to obtain cortical only and trabecular + cortical specimens, respectively, b) the ensuing CT structural rigidity analysis and c) uni-axial mechanical testing (OVX, ovariectomized; NFR, partially nephrectomized; CON, control).
Specimen preparation
After dissection and cleaning of all adherent soft tissues, a mid-diaphyseal (cortical bone only) and a distal metaphyseal (trabecular + cortical bone) specimen were cut from each femur perpendicular to the anatomical axis using two parallel diamond wafering blades on a low-speed saw (Isomet, Buehler Corporation, Lake Bluff, Illinois) under copious irrigation. The cortical midshaft specimens (height: 5.99 mm (sd 0.28), diameter at mid-length: 3.64 mm (sd 0.24)) were cut to maintain an approximate 2:1 height to diameter ratio,15 while the distal metaphyseal segments (height: 6.22 mm (sd 0.73), diameter at mid-length: 4.84 mm (sd 0.41)) were cut from the growth plate, as identified from anteroposterior contact radiographs, in order to include the distal metaphyseal trabecular micro-structure. The metaphyseal cortex was shaved off at the laboratory using diamond wafering blades under magnified viewing and ample lighting in order to obtain trabecular only specimens.13 The specimens were held by the operator’s hand, allowing much greater freedom of movement than using a jig.
Micro-CT imaging
Sequential transaxial images through the entire cortical and trabecular bone sections were obtained using micro-CT (µCT) (µCT40; Scanco Medical AG, Brüttisellen, Switzerland) at an isotropic voxel size of 30 μm, integration time of 250 ms and tube voltage and current of 55 kVp and 145 µA respectively, while applying a 1200 mg.cm-3 hydroxyapatite (HA) beam hardening correction curve. Cortical and trabecular bone mineral densities (ρ, g.cm-3) were calculated using a hydroxyapatite phantom (0, 100, 200, 400 and 800 mg HA.cm-3), supplied by the manufacturer, to convert the X-ray attenuation coefficient (μ) to volumetric bone mineral density. Average and minimum cross sectional areas of the bony components of the cortical and trabecular bone specimens were calculated from the thresholded µCT images.
Structural rigidity analysis
Rigidity, the product of the bone tissue modulus of elasticity and bone cross-sectional geometry describes the structural behavior of a bone and its resistance to deformation when subjected to axial, bending or torsional loads. The bone tissue modulus (E) depends on the bone mineral density. Axial compressive relationships describing the mentioned mechanical properties of rat bone as a function of µCT-generated density were used to convert the densities to their respective axial modulus value.13 These relationships were generated from bones from a different group of animals as those used for this study. The bone geometry is represented by the cross-sectional area. The axial (EA) rigidity for each transaxial cross-section through the bone was calculated by summing the density-weighted area of each isotropic voxel (30 µm × 30 µm × 30 µm) by its position relative to the density weighted centroid16 (Fig. 2). Average (EAAVG-CTRA) and minimum EA (EAMIN-CTRA) axial rigidities were reported for each specimen. EAAVG-CTRA represents the average axial rigidity of the entire segment, whereas EAMIN-CTRA represents the axial rigidity of the entire segment at its weakest cross-section. Given that a bone is as rigid as its weakest section,7,9 and not as its average rigidity, EAMIN-CTRA should provide meaningful information into the fidelity of the normal and pathological bone.
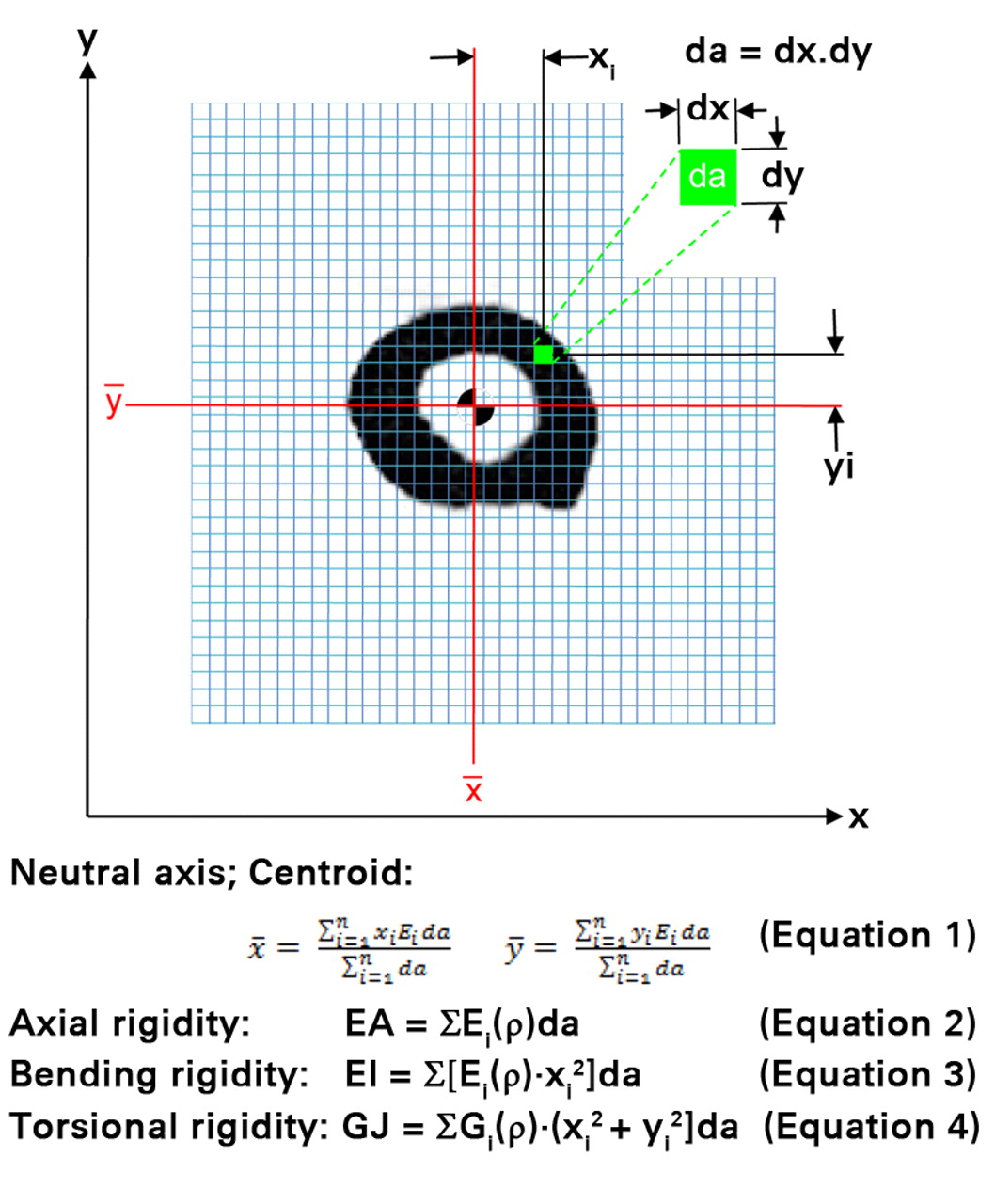
Fig. 2
A schematic diagram illustrating the pixel-based CT structural rigidity analysis technique to assess axial (EA), bending (EI) and torsional rigidities (each grid element is intended to represent one pixel).
Mechanical testing
Specimens were thawed out to room temperature and hydrated prior to mechanical testing; otherwise, they were stored in saline soaked gauze and stored at -20°C for the duration of the study. Circular brass end-caps (8 mm in diameter, 1 mm in thickness) were glued to both ends of each sample to reduce end-effect artifacts.15 Specimens were preconditioned, using a triangular waveform to 0.33% strain for 7 cycles at a strain rate of 0.005 s-1, followed by uniaxial compression to failure at a strain rate of 0.01 s-1 (Instron 8511; Instron, Norwood, Massachusetts). Yield load (LY, kN) was assessed as the point where the load-displacement curve ceased to be linear, and ultimate load (LULT, kN) was assessed as the highest load point (Fig. 3). Stress data were calculated by dividing the load with average and minimum cross sectional areas of the bony components of the cortical and trabecular bone specimens as measured from µCT images. Strain data was calculated by dividing displacement with the intact height of each specimen as measured by a caliper (average of three measurements). Modulus of elasticity, (E, N/mm), was assessed by measuring the slope of the elastic region of the stress-strain curve for the cortical and trabecular segments. Average axial rigidity (EAAVG-mech) was calculated by multiplying E (derived from mechanical testing) with the average specimen cross-sectional area (AAVG, assessed from transaxial µCT imaging, including bony sections only averaged over the entire length of the specimen). Additionally, minimum axial rigidity (EAMIN-mech) was calculated by multiplying E (derived from mechanical testing) with the minimum specimen cross-sectional area (AMIN, assessed from transaxial µCT imaging, including bony sections only and reporting the cross-sectional area with the minimum area).
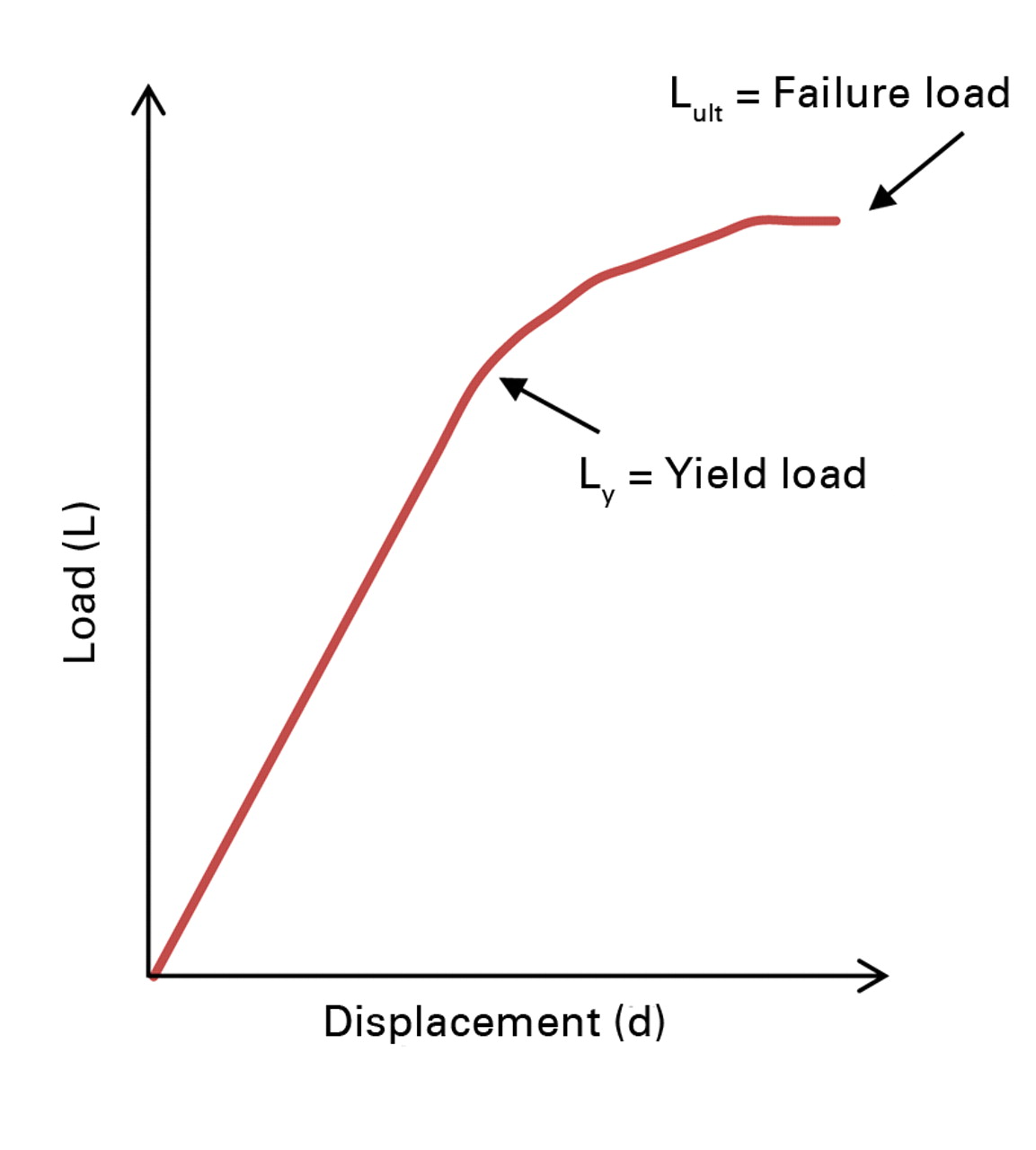
Fig. 3
Example plot of load versus displacement, illustrating the yield load (point where the curve ceases to be linear) and the ultimate load (highest load point).
Statistical analysis
Continuous data were assessed for normality using the Kolmogorov-Smirnov test. A linear regression model was applied to determine whether average and minimum axial rigidities assessed using µCT-based Structural Rigidity Analysis correlate with average and minimum EA obtained from mechanical testing. Specimens from animals with different metabolic bone diseases were analysed together, since the validity of structural rigidity analysis should depend only upon the cross-sectional geometry and density of the specimen, and not the presence or absence of a metabolic disease. A mixed model was applied to compare the intercepts and slopes since the same animals provided data on both average and minimum EA; and therefore, a repeated-measures model was needed to account for the within-animal correlation when comparing the slope and intercept parameters. Paired Student’s t-test was used to assess the correlation between EA values obtained from mechanical testing versus CTRA based average and minimum EA values respectively. Two-way analysis of variance (ANOVA) with Bonferroni post hoc analysis, with bone type (cortical and trabecular) and group (control, OVX, NFR) as fixed factors and EA parameters as dependent variables, was used to assess between bone type and group differences in the EA values. Mean values are reported with their respective standard deviation (sd) and 95% confidence interval (CI). Statistical analysis was performed using the SPSS software package (PASW Statistics v18; IBM SPSS Inc., Chicago, Illinois). Two-tailed values of p < 0.05 were considered statistically significant.
Results
All axial rigidity data generated from both CTRA and mechanical testing methods were distributed normally. CTRA and mechanical testing based average axial rigidities were well correlated with one another (EAAVG-CTRA = (1.232 × EAAVG-mech) – 3142.6; F = 159.07, p < 0.0001; Pearson correlation = 0.862 and R2 = 0.74) (Fig. 4). This correlation improved significantly when the CTRA-based EAMIN was correlated with the mechanical testing based minimum axial rigidity results (EAMIN-CTRA = (1.052 × EAMIN-mech) + 69.17; F = 297.6, p < 0.0001; Pearson correlation = 0.919 and R2 = 0.84) (Fig. 5). Tests of slopes in the mixed model regression analysis indicated a significantly steeper slope for EAAVG compared to EAMIN (p = 0.028) and a significant difference in the y-intercepts (p = 0.022).
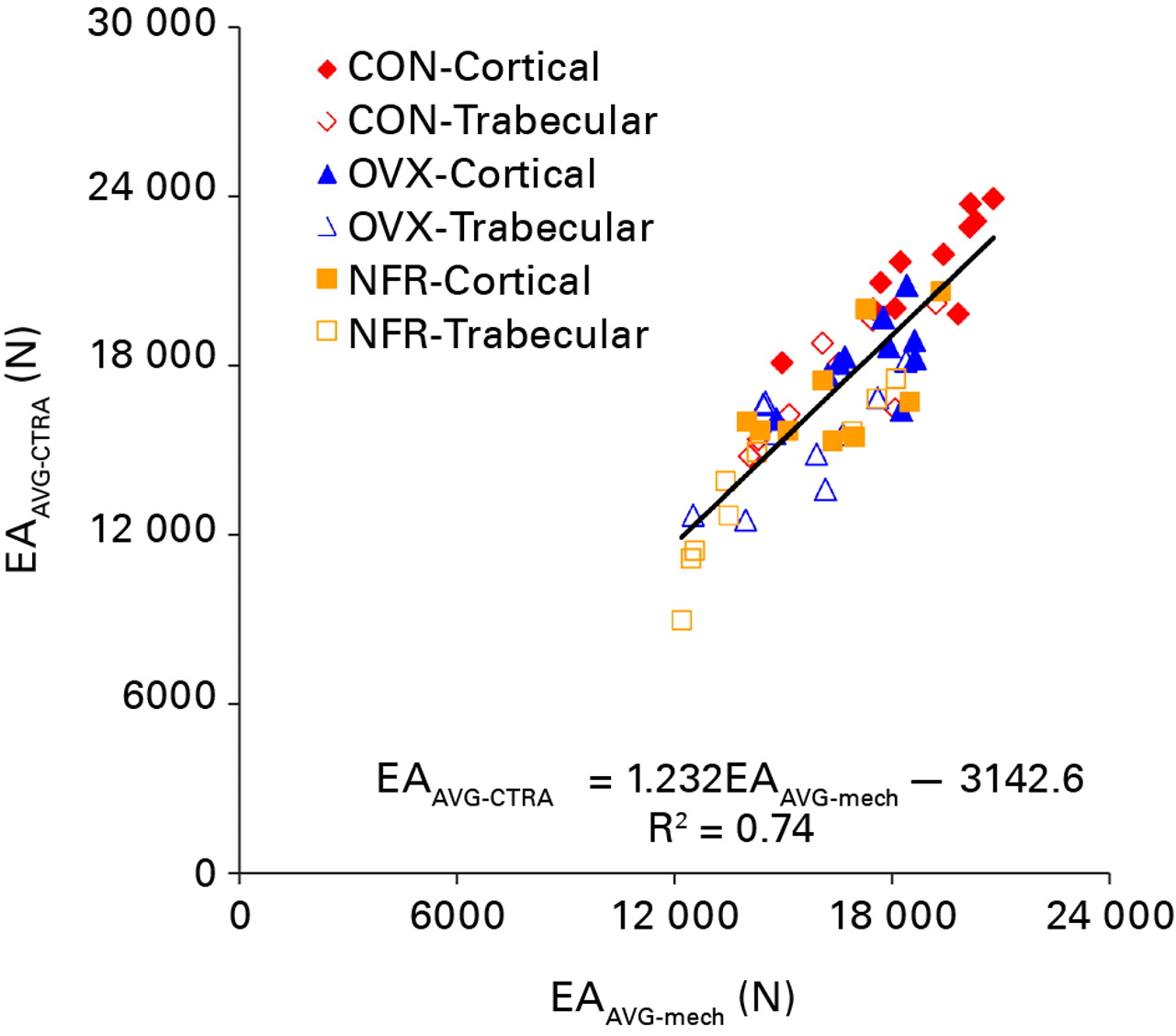
Fig. 4
Linear regression of the average axial rigidity (EA) as assessed by CT structural rigidity analysis (EAAVG-CTRA) and mechanical testing (EAAVG-mech) (CON, control; OVX, ovariectomized; NFR, partially nephrectomized).
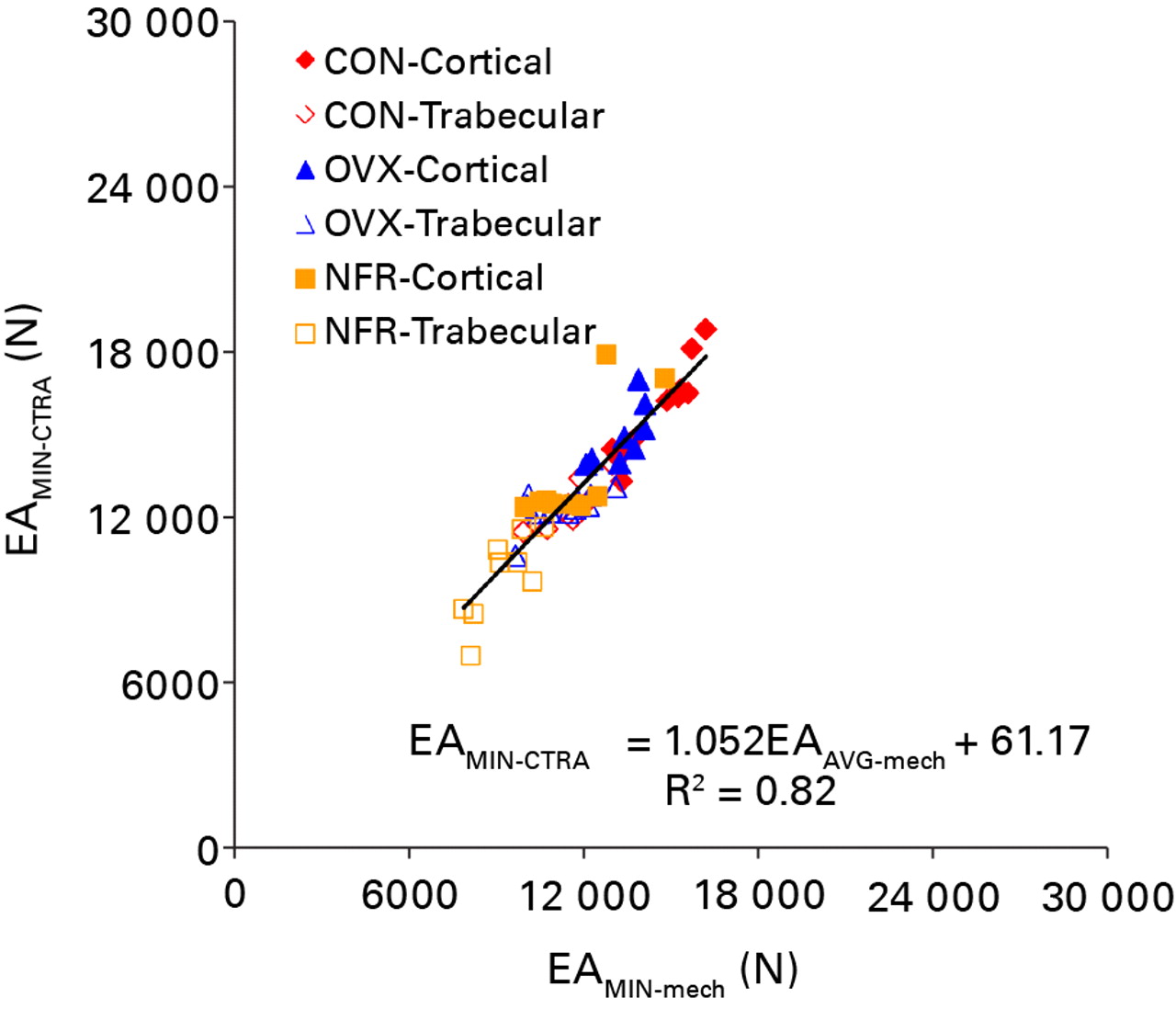
Fig. 5
Linear regression of the minimum axial rigidity (EA) as assessed by CT structural rigidity analysis (EAMIN-CTRA) and mechanical testing (EAMIN-mech) (CON, control; OVX, ovariectomized; NFR, partially nephrectomized).
The CTRA-based average and minimum axial rigidities were correlated with the mechanical testing based average and minimum axial rigidities using a paired t-test analysis (p = 0.37 and 0.18). Intra-group and intra-type t-test analysis of axial rigidity values between the control, OVX and NFR groups for both cortical and trabecular bone specimens showed correlation between the CTRA based and the mechanical testing based rigidity data (p > 0.13 for all cases).
Significant differences in EA data between different bone types (cortical versus trabecular, p < 0.0001) and groups (p < 0.0001) were observed (Table I). Post hoc analysis of the intra group differences revealed that EAAVG were not different between the OVX and NFR groups regardless of the data collection method (CTRA, p = 0.091; mechanical testing, p = 0.343). The CTRA based EAMIN results between the control and OVX groups were not significantly different from one another (p = 0.123), whereas the mechanical testing based EAMIN results between the control and OVX groups revealed a statistically significant difference (p = 0.004) (Table I). Cortical bone axial rigidity distribution occupied the upper right hand quadrant of both regression figures, whereas trabecular bone axial rigidity distribution filled the lower left quadrant of both regression figures with cortical and trabecular bones from control animals providing the highest rigidity values.
Table I
Inter-bone and inter-group presentation of the average and minimum EA data generated from CTRA analysis and mechanical testing with the two-way analysis of variance (ANOVA) and Bonferronipost hoc analysis p-values
| Mechanical testing | CTRA | ||||
|---|---|---|---|---|---|
| EAAVG (sd) [95% CI] | EAMIN (sd)[95% CI] | EAAVG (sd) [95% CI] | EAMIN (sd) [95% CI] | ||
| Cortical | |||||
| Control | 18851 (1744) | 15090 (1227) | 21462 (1873) | 15745 (1716) | |
| [17679 to 20023] | [14265 to 15915] | [2203 to 22721] | [14592 to 16898] | ||
| Ovariectomized | 17400 (1280) | 13596 (943) | 18268 (1415) | 14445 (1354) | |
| [16484 to 18315] | [12921 to 14721] | [17255 to 19280] | [13476 to 15414] | ||
| Nephrectomized | 16448 (1808) | 12197 (1537) | 16967 (2014) | 13551 (2198) | |
| [15058 to 17837] | [11015 to 13379] | [15419 to 18516] | [11862 to 15241] | ||
| Trabecular | |||||
| Control | 16368 (1840) | 11957 (940) | 17408 (2018) | 12338 (861) | |
| [14830 to 17907] | [11170 to 12743] | [15720 to 19095] | [11617 to 13058] | ||
| Ovariectomized | 15487 (1794) | 11418 (1137) | 15276 (1894) | 12179 (650) | |
| [14203 to 16771] | [10604 to 12231] | [13921 to 16632] | [11714 to 12644] | ||
| Nephrectomized | 14541 (2360) | 9556 (1028) | 13626 (2864) | 9763 (1546) | |
| [12727 to 16356] | [8765 to 10347] | [11424 to 15827] | [8574 to 10952] | ||
| ANOVA p-value | |||||
| Bone | < 0.0001 | < 0.0001 | < 0.0001 | < 0.0001 | |
| Group | 0.004 | < 0.0001 | < 0.0001 | < 0.0001 | |
| Bonferroni post hoc p-values | |||||
| Control vs ovariectomized | 0.07 | 0.004 | < 0.0001 | 0.123 | |
| Control vs nephrectomized | 0.001 | < 0.0001 | < 0.0001 | < 0.0001 | |
| Ovariectomized vs nephrectomized | 0.343 | < 0.0001 | 0.091 | 0.004 | |
Discussion
Despite continued development of new therapies and treatments to prevent and treat fragility fractures, accurate, non-invasive assessment of fracture risk remains an elusive task. The results of this study support thehypothesis that axial rigidity of bones with metabolic pathologies can be accurately and quantitatively assessed in a rat model by conducting structural rigidity analysis on serial axial images of the affected bone. Axial rigidity measured non-invasively by µCT was well correlated with the results from mechanical testing as the gold standard measure. Minimum axial rigidity produced a stronger correlation with mechanical testing based minimum rigidity results (R2 = 0.84) than their average counterparts (R2 = 0.74). Furthermore, intra-group and intra-type paired Student’s t-test showed no significant difference in axial rigidity as determined by CTRA and mechanical testing (p > 0.13 for all cases).
In the average axial rigidity model, the slope of the linear regression was 1.23 and the y-intercept offset was 3142, suggesting that CTRA using average axial rigidity consistently over-predicts bone rigidity. In the minimum axial rigidity model, the slope of the linear regression was 1.05 and the y-intercept offset was 69, indicating that CTRA is correlated without much skewness with mechanical testing results over the full range of the values tested. This data lends further support to the hypothesis that minimum rigidity is more accurate than average rigidity in predicting the overall rigidity of bone.
The cortical bone specimens predominantly make up the upper right quadrant of each regression model, corresponding to higher rigidity. Concurrently, trabecular bone specimens occupy the lower left quadrant of each regression model, corresponding to their lower rigidity distribution. In both cases, cortical and trabecular bones from partially nephrectomized animals comprise the lowest axial rigidity combination along the regression line of each bone type, while bones from ovariectomized animals comprise the mid-range for axial rigidity values from both bone types followed by bones from control animals.
In other studies, it has been shown that µCT and peripheral quantitative CT data in diabetic rats will identify changes in both bone densities and structure which then ultimately correlates with decreased structural strength and increased fragility in affected bones.17 Another study used µCT to assess BMD in ovariectomized sheep and found that the corresponding change in the BMD and trabecular micro-architecture correlated with changes in the mechanical properties of the osteopenic bone; specifically the trabecular thickness and the bone volume fraction.18 Recently, one group used µCT in vivo to monitor the effect of zoledronic acid on the micro-architecture of ovariectomized rats; demonstrating the ability of µCT to detect crucial changes in bone volume fraction, trabecular number, and trabecular thickness, which ultimately correlate with bone strength.19
This study proposes that not only is there a correlation between µCT-derived data and bone rigidity, but that structural rigidity analysis based on µCT data can be successfully employed to non-invasively assess the axial rigidity of bones with metabolic pathologies. Ultimately, the advantage of this technique is that it uses structural engineering principles to calculate rigidity of bone, rather than using simple scalar measures such as density or morphometric indices that may provide good correlation but may not be based on theory.
The CTRA based average and minimum axial rigidities were compared to average and minimum axial rigidity values obtained from mechanical testing. This process entailed the assessment of E from the slope of the stress-strain curve followed by assessment of average and minimum bony cross-sectional areas from µCT images. This was done in order to generate equivalent rigidity indices to compare those that took into account changes in bony area measurement for both CTRA and mechanical testing methods. Failure load from mechanical testing, which have a unit of force as well, could have been used to correlate with the CTRA based average and minimum axial rigidity values, which would have been a more direct measurement. Additionally, torsional rigidity would have been a better option to use in a long bone setting. However, axial rigidity was chosen instead to generate rigidity data for both cortical and trabecular components of the bone, given that metabolic diseases affect the two bone types differently. The results suggest that the CTRA analysis was capable of differentiating between the bone types and groups as shown in Table I.
In summary, the results of this study suggest that structural rigidity analysis of µCT data can be used to accurately and quantitatively measure the axial rigidity of bones with metabolic pathologies in an experimental rat model. As shown, minimum axial rigidity appears to be a better model for measuring bone rigidity than average axial rigidity. It remains to be seen whether analogous CT images in human patients could also be used to predict fracture risk in those affected by metabolic bone diseases. Future studies across multiple disease models and imaging techniques involving larger sample sizes is warranted to evaluate the reproducibility and extensibility of these promising results. However, the results of this study suggest considerable potential in the use of µCT-based CTRA to quantitatively and non-invasively assess load bearing capacity of bones with metabolic diseases.
The authors would like to acknowledge the Komen Foundation for providing financial support for this project (BDS Grant No: BCTR0403271). The authors would also like to acknowledge Mr. F. Araiza from The Center for Advanced Orthopaedic Studies for his help with the references and formatting of the manuscript.
1 Riggs BL , LJ Melton 3rd. The worldwide problem of osteoporosis: insights afforded by epidemiology. Bone1995;17(Suppl):505–511.CrossrefPubMed Google Scholar
2 LeBoff MS , KohlmeierL, HurwitzS, et al.Occult vitamin D deficiency in postmenopausal US women with acute hip fracture. JAMA1999;281:1505–1511.CrossrefPubMed Google Scholar
3 Sokoloff L . Occult osteomalacia in American (U.S.A.) patients with fracture of the hip. Am J Surg Pathol1978;2:21–30.CrossrefPubMed Google Scholar
4 Turner CH . Determinants of skeletal fragility and bone quality. J Musculoskelet Neuronal Interact2002;2:527–528.PubMed Google Scholar
5 No authors listed. Assessment of fracture risk and its application to screening for postmenopausal osteoporosis: report of a WHO Study Group World Health Organ Tech Rep Ser1994;843:1–129. Google Scholar
6 Schuit SC , van der KliftM, WeelAE, et al.Fracture incidence and association with bone mineral density in elderly men and women: the Rotterdam Study. Bone2004;34:195–202.CrossrefPubMed Google Scholar
7 Snyder BD , Hauser-KaraDA, HippJA, et al.Predicting fracture through benign skeletal lesions with quantitative computed tomography. J Bone Joint Surg [Am]2006;88-A:55–70.CrossrefPubMed Google Scholar
8 Whealan KM , KwakSD, TedrowJR, InoueK, SnyderBD. Noninvasive imaging predicts failure load of the spine with simulated osteolytic defects. J Bone Joint Surg [Am]2000;82-A:1240–1251.CrossrefPubMed Google Scholar
9 Hong J , CabeGD, TedrowJR, HippJA, SnyderBD. Failure of trabecular bone with simulated lytic defects can be predicted non-invasively by structural analysis. J Orthop Res2004;22:479–486.CrossrefPubMed Google Scholar
10 Miller SC , WronskiTJ. Long-term osteopenic changes in cancellous bone structure in ovariectomized rats. Anat Rec1993;236:433–441.CrossrefPubMed Google Scholar
11 Kazama JJ , IwasakiY, YamatoH, et al.Microfocus computed tomography analysis of early changes in bone microstructure in rats with chronic renal failure. Nephron2003;95:152–157.CrossrefPubMed Google Scholar
12 Nazarian A , CoryE, MüllerR, SnyderBD. Shortcomings of DXA to assess changes in bone tissue density and microstructure induced by metabolic bone diseases in rat models. Osteoporosis Int2009;20:123–132.CrossrefPubMed Google Scholar
13 Cory E , NazarianA, EnteraziV, et al.Compressive axial mechanical properties of rat bone as functions of bone volume fraction, apparent density and micro-ct based mineral density. J Biomech2010;43:953–960.CrossrefPubMed Google Scholar
14 Miller MA , ChinJ, MillerSC, FoxJ. Disparate effects of mild, moderate, and severe secondary hyperparathyroidism on cancellous and cortical bone in rats with chronic renal insufficiency. Bone1998;23:257–266.CrossrefPubMed Google Scholar
15 Keaveny TM , BorchersRE, GibsonLJ, HayesWC. Theoretical analysis of the experimental artifact in trabecular bone compressive modulus. J Biomech1993;26:599–607.CrossrefPubMed Google Scholar
16 Lai WM, Krempl E, Rubin D. Introduction to continuum mechanics. Third ed. Waltham: Butterworth-Heinemann, 1993. Google Scholar
17 Reinwald S , PetersonRG, AllenMR, BurrDB. Skeletal changes associated with the onset of type 2 diabetes in the ZDF and ZDSD rodent models. Am J Physiol Endocrinol Metab2009;296:765–774.CrossrefPubMed Google Scholar
18 Mittra E , RubinC, QinYX. Interrelationship of trabecular mechanical and microstructural properties in sheep trabecular bone. J Biomech2005;38:1229–1237.CrossrefPubMed Google Scholar
19 Gasser JA , IngoldP, VenturiereA, ShenV, GreenJR. Long-term protective effects of zoledronic acid on cancellous and cortical bone in the ovariectomized rat. J Bone Miner Res2008;23:544–551.CrossrefPubMed Google Scholar
Funding statement:
None declared
Author contributions:
M. D. Smith: Manuscript preparation
S. Baldassarri: Data collection
L. Anez-Bustillos: Manuscript preparation, data analysis
A. Tseng: Data collection
V. Entezari: Data analysis
B. D. Snyder: Study design
A. Nazarian: Study design, data collection, data analysis, manuscript preparation
D. Zurakowski: Data analysis
ICMJE Conflict of Interest:
None declared
©2012 British Editorial Society of Bone and Joint Surgery. This is an open-access article distributed under the terms of the Creative Commons Attributions licence, which permits unrestricted use, distribution, and reproduction in any medium, but not for commercial gain, provided the original author and source are credited.










